• Mejor legibilidad

Arboles de decisiones

• Los árboles de decisión son un algoritmo de aprendizaje supervisado que se utiliza para problemas de clasificación y regresión.
• Son conocidos por su simplicidad y facilidad de interpretación de arbol.
• Los árboles de decisión son un tipo de modelo predictivo que mapea características (variables independientes) a conclusiones sobre la variable dependiente.
• Imagina que estás intentando ver si jugar tenis dependiendo del clima. Un árbol de decisión podría ser:
  • Si está soleado, jugar tenis.
  • Si está nublado, jugar tenis.
  • Si está lluvioso, no jugar tenis.
• Un arbol de decisión tiene tres componentes principales:
  1. Nodos de decisión: Representan una característica o atributo.
  2. Nodos de ramificación: Representan una regla de decisión.
  3. Nodos de hoja: Representan el resultado.

Armando un árbol de decisión

• Involucra seleccionar la mejor característica para dividir los datos en cada nodo.
• Esta selección está basada en cuestiones como gini impurity, entropy o information gain.
• Que cuantifica la homogeneidad de cada subconjunto resultando de la división.
• La idea es crear divisiones que resulten en incrementar mas subconjuntos puros o homogéneos. Donde los data points de cada subconjunto sean lo mas similares posible.

Impuridad de Gini

• La impureza de Gini es una medida de cuán a menudo un elemento elegido al azar sería incorrectamente clasificado.

\(Gini(s) = 1 - \sum_{i=1}^{n} (p_i)^2\)

• Donde:
  • $s$ es el conjunto de datos.
  • $n$ es el número de clases.
  • $p_i$ es la probabilidad de elegir una clase $i$.
• Considerar el data set s que contiene elementos de dos clases, $A$ y $B$.
• Supon que hay 30 instancias de $A$ y 20 instancias de $B$.
  • Proporción de clase $A$: $\frac{30}{50} = 0.6$
  • Proporción de clase $B$: $\frac{20}{50} = 0.4$
• Ahora si hacemos la impureza de Gini:
  • $Gini(s) = 1 - (0.6)^2 - (0.4)^2 = 0.48$

Entropía

• La entropía es una medida de la incertidumbre asociada con un conjunto de datos.

\(Entropy(s) = - \sum_{i=1}^{n} p_i \log_2(p_i)\)

• Donde:
  • $s$ es el conjunto de datos.
  • $n$ es el número de clases.
  • $p_i$ es la probabilidad de elegir una clase $i$.
• Usando la misma S que antes podemos calcular la entropía:
  • $Entropy(s) = -0.6 \log_2(0.6) - 0.4 \log_2(0.4) = 0.97$

Information Gain o Ganancia de Información

• La ganancia de información es la medida de la reducción de la entropía o impureza después de dividir un conjunto de datos en un subconjunto.

\(IG(S,A) = Entropy(S) - \sum_{t \in T} \frac{|t|}{|S|} Entropy(t)\)

• Donde:
  • $S$ es el conjunto de datos original.
  • $A$ es la característica que divide los datos.
  • $T$ es el subconjunto de $S$ después de dividir $S$ usando la característica $A$.

  • $

    t

    $ es el número de instancias en el subconjunto $t$.

  • $

    S

    $ es el número de instancias en el conjunto de datos original.

• Considerando a $S$ como el dataset con 50 instancias, tomando las dos clases consideramos $F$ que puede tomar en dos valores $1$ y $2$.
• La distribución sería:
  • $F = 1$: 30 instancias, 20 clase $A$ y 10 clase $B$.
  • $F = 2$: 20 instancias, 10 clase $A$ y 10 clase $B$.
• Primero calculamos la entropía de $S$:
  • $Entropy(S) = -0.6 \log_2(0.6) - 0.4 \log_2(0.4) = 0.97$
• Luego calculamos la entropía del subconjunto $T$:
  • para $F = 1$: $Entropy(T) = -0.67 \log_2(0.67) - 0.33 \log_2(0.33) = 0.92$
  • para $F = 2$: $Entropy(T) = -0.5 \log_2(0.5) - 0.5 \log_2(0.5) = 1.0$
• Ahora calculamos el promedio ponderado de la entropía de los subconjuntos:
  • Weighted Entropy = $\frac{30}{50} \times 0.92 + \frac{20}{50} \times 1.0 = 0.94$
• Finalmente calculamos la ganancia de información:
  • $IG(S,F) = 0.97 - 0.94 = 0.03$

Armando el arbol

• El arbol empieza con la raíz, que contiene el dataset completo.
• Luego se divide en subconjuntos mas pequeños con el criterio ( Gini, Entropía o Information Gain).
• Se sigue dividiendo hasta que se llega a un nodo hoja, que contiene la clase final.
• Este proceso es recursivo y se detiene cuando se alcanza un criterio de parada.
• las tres paradas de crecimiento comunes son:
  1. Profundidad máxima del árbol: El arbol alcanza la profundidad maxima especificada.
  2. Numero minimo de puntos de datos en un nodo: El numero de puntos de datos en un nodo cae por debajo de un umbral especificado, asegurando que las divisiones son significativas y no esten basadas en un pequeño numero de puntos de datos.
  3. Nodos puros: Todos los puntos de datos de un nodo pertenecen a la misma clase, indicando que mas divisiones no ayudan a mejorar la predicción.

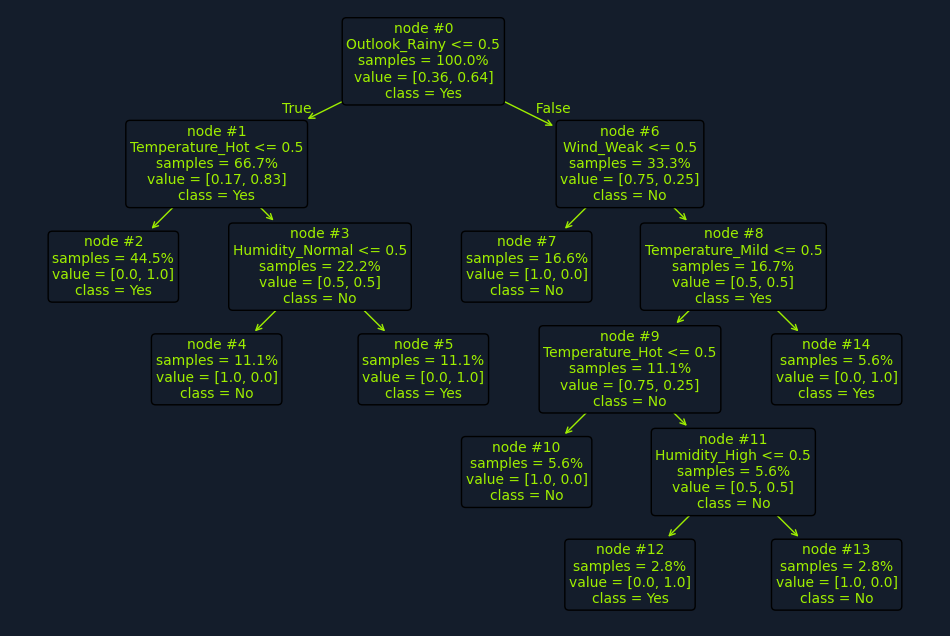
• imagina que tenemos el dataset historico del clima y si se jugo tenis o no.

JugarTenis	Nublado	Lluvioso	Soleado	Frío	Caliente	Templado	Humedad_Alta	Humedad_Normal	Viento_Fuerte	Viento_Débil
No	Falso	Verdadero	Falso	Verdadero	Falso	Falso	Falso	Verdadero	Falso	Verdadero
Sí	Falso	Falso	Verdadero	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero
No	Falso	Verdadero	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero	Falso
No	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero	Falso	Falso	Verdadero
Sí	Falso	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero	Falso	Verdadero
Sí	Falso	Falso	Verdadero	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero
No	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero	Falso	Verdadero	Falso
Sí	Verdadero	Falso	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Falso	Verdadero
No	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Falso	Verdadero	Verdadero	Falso
No	Falso	Verdadero	Falso	Falso	Verdadero	Falso	Verdadero	Falso	Verdadero	Falso

• Clima: soleado, nublado, lluvioso.
• Temperatura: caliente, templado, frío.
• Humedad: alta, normal.
• Viento: fuerte, débil.

• la variable objetivo es si se jugó tenis o no.

• un arbol de decisión analizaría las características y dividiría el dataset en subconjuntos mas pequeños.
• Empezaría por calcular cada impureza de Gini o entropía para cada característica y seleccionar la que resulte en la mayor ganancia de información.
• Por ejemplo, si la característica que resulta en la mayor ganancia de información es el clima, el arbol se dividiría en tres ramas: soleado, nublado y lluvioso.
• Luego, el arbol se dividiría en subconjuntos mas pequeños basados en las características restantes.
• Este proceso se repite hasta que se llega a un nodo hoja, que contiene la clase final.

Asunciones de los árboles de decisión

• Una de las ventajas de los árboles de decisión es que no requieren muchas asunciones.
• No linealidad: Los árboles de decisión pueden capturar relaciones no lineales entre las características y la variable objetivo.
• No normalidad: Los árboles de decisión no requieren que las características sigan una distribución normal.
• No escala: Los árboles de decisión no requieren que las características estén en la misma escala.